Lexical Analysis/词法分析
词法分析器的功能
- 将字符流转换成记号流,提供给语法分析器使用
- 去除源程序的注解、空白,如果源程序语言支持宏定义,词法分析器也可以负责将宏定义展开
- 将编译器各个阶段的错误信息与源程序联系起来,由于词法记号流不存在行的概念,因此可以由词法分析器记住当前所处的行号,从而将错误信息对应的行位置确定
词法记号、模式、词法单元
词法记号
定义
token/词法记号号是一类符合相同模式的词法单元的统称,实际上记号包含记号名和属性,而前者是一类词法单元的抽象名字,后者是可选的(可以没有)
即 token = <token_name,attribute_value>
词法记号的属性
用于在记号的二元组内记住记号的信息,从而翻译记号。某些记号可以没有属性值,因为其记号名足以指示如何翻译这个记号。
例如下列代码中:
position = initial + 60*rate
记号二元组包括:<id,指向符号表中position条目的指针><assign_op><id,指向符号表中initial条目的指针><add_op><number,整数值60><mul_op><id,指向符号表中rate条目的指针>
记号名影响语法决策,而属性影响如何翻译
模式
pattern/模式描述了某一记号的字符串的构成规则
词法单元
lexeme/词法单元(也称词素、单词)是词法记号的实例,即匹配某个记号模式的字符序列
三者关系举例
例如记号名叫做id,属于这一记号名的词法单元有sum,count这些变量名,而对这一类记号的模式的非形式化描述可以是:字母开头的字母数字串
正则表达式
串、语言
基本定义
- 字母表:符号的有限集合
- 串:符号的有穷序列。字母表上的串即该字母表内符号组成的有限集合。
- 语言:字母表上串的集合。某种语言的串又称作该语言的字或者句子。
语言的运算
- $L \cup M ={ s \mid s\ \in L\ or\ s\ \in M }$,即语言的并
- $LM = { st \mid s \in L\ and\ t \in M }$,即语言的连接
- $L^* =\bigcup_{i=0}^{\infty}L^i$,即零个或多个L句子的连接的并
- $L^+ =\bigcup_{i=1}^{\infty}L^i$,即一个或多个L句子的连接的并
正规式
基本定义
一组定义规则,这组定义规则描述了串的模式,即串模式的形式化描述。每个正规式$r$代表了一种语言$L(r)$,说明了$L(r)$中的句子是如何由$r$构造的,正规式表示的语言叫做正规语言或正规集。
区别正规式和句子:句子是串,而相应的正规式是描述这个串的模式的规则,例如某正规式r=a,那么$L(r) = {a}$,并且a是该语言的一个句子,虽然正规式和这里提到的这个句子都用a表示,但他们本质不同
正规式包含的运算
若$r,s$都是正规式,那么它们的运算和对应关系如下
- $r\mid s = L(r) \cup L(s)$,该运算称为选择
- $rs = L(r)L(s)$,该运算称为连接
- $r^* = L(r)^*$,该运算称为闭包
- $r^+ = L(r)^+$,该运算称为正闭包
- $r = s \iff L(r)=L(s)$,即两正规式等价等价于它们表示的语言相同
各算符均是左结合的,并且优先级闭包、正闭包相等,大于连接运算,大于选择运算
正规定义
正规定义指将正规式用名字进行命名,并在后续的定义中通过引用这些名字来引用正规式。一般形式为如下定义序列
$name_1 \to r_1$
$name_2 \to r_2$
$…$
$name_n \to r_n$
其中$r_i \in \sum \cup { r_1,r_2,…,r_{i-1}}$
注意:正规定义是不允许递归定义的,且正规定义只能引用已经定义好的正规定义。
有限自动机
即识别器程序实现的逻辑模型,可以认为是正规式或者是模式的图形化,其可以用状态转换图或者状态转换矩阵(表格)来描述
基本概念
状态转换图表示
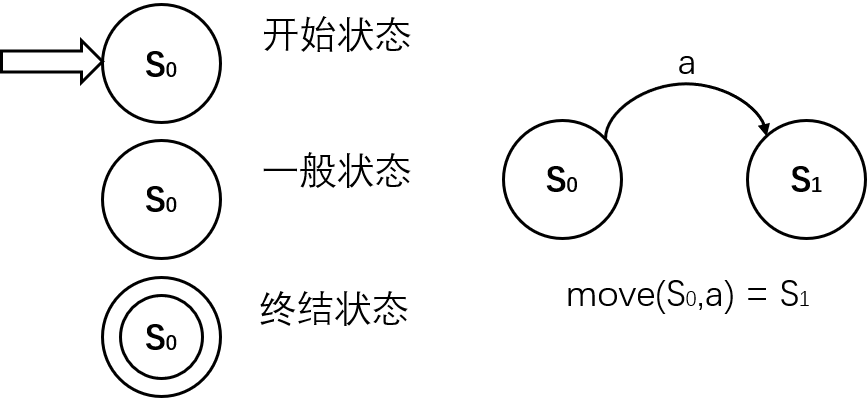
有限自动机识别的语言
$\alpha$是某FA识别(接受)的串 $\iff$ $\exists$一条从FA初态到某个终态的状态转换路径,该路径上所有标记的字符序列为$\alpha$
FA识别(接受)的语言指的FA识别(接受)的串的集合,记为$L(M)$
NFA
NFA(Non-deterministic Finite Automata)是一个数学模型$(\sum, S,s_0,F,move)$,该五元组的各部分意义如下:
- 一个有限的状态集合$S$
- 唯一的初始状态$s_0 \in S$
- 终止(接受)状态$F\subseteq S$
- 输入符号集(输入字母表)$\sum$,要注意空串$\epsilon$是不会出现在输入字母表里的
- 状态转移函数$move:S \times (\sum \cup \epsilon) \to P(S)$,其中$P(S)$是有限状态集合$S$的幂集(即所有子集)
DFA
DFA是NFA的特殊情况,其与NFA的区别在于:
- 不存在$\epsilon$转化
- 状态转移函数$move:S \times \sum \to S$,即为单值函数,任意状态通过某转化最多只能转移到一个状态
- 对相同的属于字母表$\Sigma$的串,DFA识别路径唯一而NFA不唯一
NFA一般而言可以直接从正则式推出,其制作的识别器要慢于DFA,但是其状态数相对DFA更少,因此所使用的存储空间更小 {.:notice–info}
正则式与NFA或DFA
$\sum$ 上的NFA $\iff \sum$ 上的正规式R,即对$\sum$上的NFA,一定存在一个NFA,使得$L(R)=L(M)$,反之亦然。
另外,由于NFA一定可以化为DFA,因此实际上$R,NFA,DFA$是等价的(不能认为是一一对应的,因为状态机可以有多种形式),后两者识别语言的能力是相同的,但是效率不同
Tompson方法
即将正则式转化到NFA的一套固定对应关系。这种方法是自底向上,从左到右的,并且是递归的,对应关系如下图
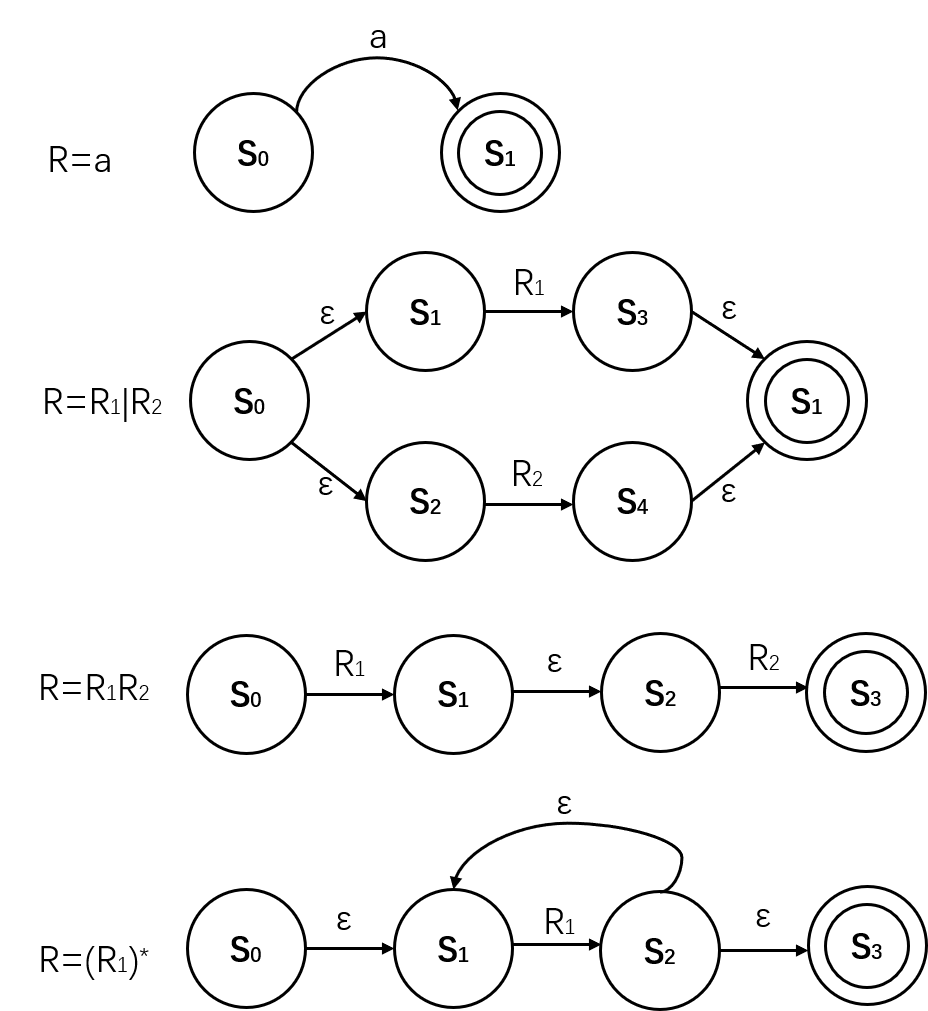
注:上面$R = (R1)^*$应该在$S_0,S_3$之间加一个从前者者到后者的空转换,因为闭包包括空串。
例如图中对于连接运算生成相应NFA,并递归地调用对其中$R_1,R_2$转换的生成过程,最终递归结束时是由最内层递归不断向上一层返回的。
简化方法
可以对正规式自顶向下进行分解,即先将整个正规式作为一个整体转化,然后将最外层转换分离单独作为一个转换,因此可以采用循环的结构(或者尾递归),自顶向下进行
例如对正规式$(0|1)^*1$的自顶向下构造如下图
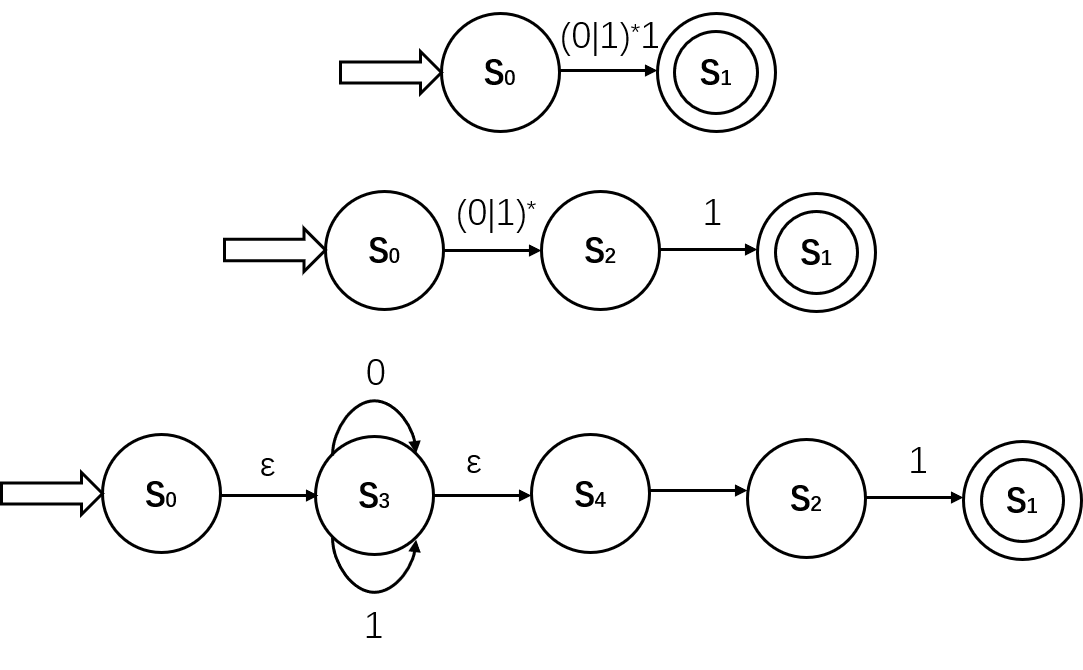
从FA到正规式
没有固定方法,转化时考虑将FA某一部分合成一个正规式,并作为一个整体接着与其他正规式合并。
NFA到DFA的转化
NFA到DFA的方法称为子集构造法。
核心思想:将NFA中状态集合的子集组成新的状态作为DFA中的状态,这些状态是上一新状态中原状态通过同一转化得到的,它们和它们任意次空转换得到的状态合在一起得到一个新状态,最终各状态之间的转移符合DFA定义(即无空转换并且转换函数为单值) 。
算法描述
输入:一个NFA
输出:一个DFA,并且其和输入的NFA接受相同的语言
算法:
while(there exists unsigned state T in Newstates[])
for each input sign a
D = $\epsilon-closure$(move(T,a))
if(D not in Newstates[]) Add D into Newstates[]
newmove[T,a] = D
具体例子可参考《编译原理》p44例子
DFA化简
每一个正规集都可以由一个状态最少(最简)的DFA识别,并且这个DFA是唯一的(证略)
核心思想:从粗粒度到细粒度对状态集合进行划分,划分的依据是能否区分同一集合内的状态,两个状态能区分指以下含义:
- 接受状态和非接受状态是一定可以区分的(初始时即可划分在两个集合内)
- 如果两个状态通过$\sum$上任意转化到达的集合是彼此相同的,那至少当前这两个状态无法被区分,它们仍旧处于同一集合
算法描述
输入:一个DFA M
输出:一个DFA M’,其和M接受相同的语言并且状态数最少
算法:
- 初始划分$\Pi$:添加死状态(指可以从初始状态到达但是一旦到达就无法前往接受状态的状态,该状态所有转换均到自身)把转换函数变为全函数,将M的状态划分成接受子集$F$和非接受子集$S$。
- for each set G in $\Pi$
state s,t are remains together if and only if for each input sign a, move(s,a),move(t,a) are in same set
if($\Pi == \Pi_{new}$) break
$\Pi = \Pi_{new}$ - 将包含M初始状态的集合作为新的初始状态,将包含M接受状态的集合作为新的接受状态,并去除死状态和无法通过初始状态到达的状态(指原来的状态的集合构成的新状态),构造M’
最终得到的新状态集合一定满足要么只含原来的接受状态,要么不含原来的接受状态。
Q:为什么化简之前要利用死状态将转换函数变为全函数?如果不是全函数为什么化简之后DFA可能接受不同的语言?