1.多项式表示

1.1.系数表示

​ 多项式的系数表示即用各次项的系数来唯一的表示多项式，例如$A(x) = a_0+a_1x+…+a_{n-1}x^{n-1}$，系数表示为：

​ $(a_0,…,a_{n-1})$

1.2.点值表示

​ n次多项式可由其上n个不同的点的值唯一确定，这n个点的集合称为该n次多项式的点值表示。如果用矩阵表达，如下：

2.离散傅里叶变换

​ 若$A(x) = a_0+a_1x+…+a_{n-1}x^{n-1}$，那么记$y_k = A(\omega_n^k)$，其中$\omega_n = e^{\frac{2\pi i}{n}}$，那么称： \((y_0,...,y_k)\) ​ 为$(a_0,…,a_{n-1})$的离散傅里叶变换(DFT)。

3.快速傅里叶变换(FFT)

3.1.基本思路

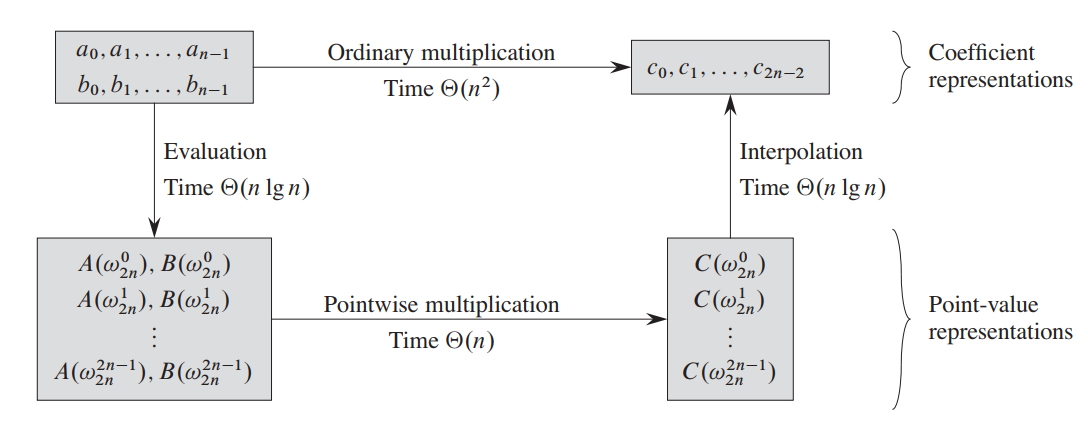
​ 通过挑选特定的$2n$个点，在$\Theta(nlgn)$时间内完成从系数表示到特定点的点值表示的变换，从而在$\Theta(n)$时间内完成点值表示的多项式乘法，如果需要得到系数表示，再通过这$2n$个特殊的点在$\Theta(nlgn)$时间内完成插值。

​ 在$\Theta(nlgn)$时间内完成$DFT_n(a)$计算的方法叫做FFT，在$\Theta(nlgn)$时间内完成$DFT_n^{-1}(a)$计算的方法叫做逆FFT。

3.2.递归实现

​ 基本原理为：$A(x)$可以表示为如下形式：(这里均假设n为2的整数次幂) \(A(x) = A^{[0]}(x^2)+xA^{[1]}(x^2) \\ A^{[0]}(x) = a_0+a_2x+...+a_{n-2}x^{\frac{n}{2}-1} \\ A^{[1]}(x) = a_1+a_3x+...+a_{n-1}x^{\frac{n}{2}-1}\) ​ 如果$x = \omega_n^k$，由于$\omega_n^k = -\omega_n^{k+\frac{n}{2}}$，故原来对n个点的DFT变为求两次n/2个点的DFT。即在求解过程中，$A^{[0]}((\omega_n^{k})^2) = A^{[0]}((\omega_n^{k+\frac{n}{2}})^2)$，因此可以重复利用，对$A^{[1]}$同理。

3.3.迭代实现

​ 迭代实现依据为蝶形网络，需要通过rev()函数把原本按照$a_0,a_1,…,a_{n-1}$排列的向量变为蝶形网络对应的排列顺序，即按位反转。