红黑树

定义

红黑树是一种二叉排序树，并且带有自平衡的特征，与平衡二叉排序树“严格”自平衡不同，红黑树只要求黑色完美平衡
一棵红黑树满足以下性质：

  1. 其节点要么是红色要么是黑色
  2. 其根节点是黑色的
  3. 叶子节点是黑色的，并且其值为NIL
  4. 红色节点的孩子只能是黑色，黑色节点的孩子可以是红色或者黑色
  5. 每个内部节点到其为根形成的子树的所有叶子节点的简单路径上，黑色节点的数量是一样的(黑色完美平衡)

由5得到推论5.1：如果一个节点有一个黑色的孩子，那么其必然有两个孩子，另一个孩子可以是黑色或者红色

时间复杂度

包含N个节点的红黑树查找的最坏时间复杂度为O(logN)

推导

  1. 首先考虑黑色高度为bh的红黑树至少有多少节点，显然最少情况是不包含红色节点，黑色节点形成一棵黑色平衡的树，节点数量为2bh-1，因此实际节点数量的下界是2bh-1
  2. 然后考虑黑色高度和高度的关系，由于红色节点的孩子必须是黑色节点，所以加入红色节点最多的情况是和黑色节点交替形成各层，此时h=2bh，其余情况下，bh>h/2，故bh>=h/2
  3. 综上，红黑树满足
    N >= 2bh-1 >= 2h/2-1
    故有h <= 2log(N+1)

红黑树的操作

红黑树部分操作涉及到自平衡，自平衡主要靠左旋、右旋、变色三种手段进行

查找

红黑树的查找与普通的二叉排序树类似，最坏时间复杂度已经在上面给出
查找步骤这里省略，递归进行即可

插入

插入时各种情况的出现基于以下两个事实：

  1. 插入节点应该是红色的，因为红色不会破坏黑色完美平衡，插入黑色节点会带来不必要的麻烦
  2. 插入节点应是一个叶子(除非树本身为空)，其位置由查找确定，其双亲(如果有)决定了这次插入是否合法，例如双亲是红色那么需要做出相应调整

    情况1：空树

    直接将插入节点作为根，并改为黑色

    情况2：插入节点已存在于树中

    不对树做任何修改

    情况3：双亲节点是黑色

    直接插入即可

    情况4：双亲节点是红色

    这种情况下的插入势必需要用到变色的技巧，否则不符合红黑树的定义

    情况4.1：双亲节点有兄弟节点

    首先需要明确一点：双亲的兄弟必然是红色，而双亲的双亲必然是黑色(只有这样才能在双亲是红色的情况下符合红黑树定义)
    处理方法：将双亲和双亲的兄弟变为黑色，将双亲的双亲变为红色，然后将双亲的双亲作为刚刚插入的节点，递归地进行插入即可，图示如下。
    图中标出了双亲是双亲的双亲左孩子，插入位置是双亲左孩子的情况，对于其他类似的情况可以类比(例如插入位置是双亲右孩子，双亲是双亲的右孩子)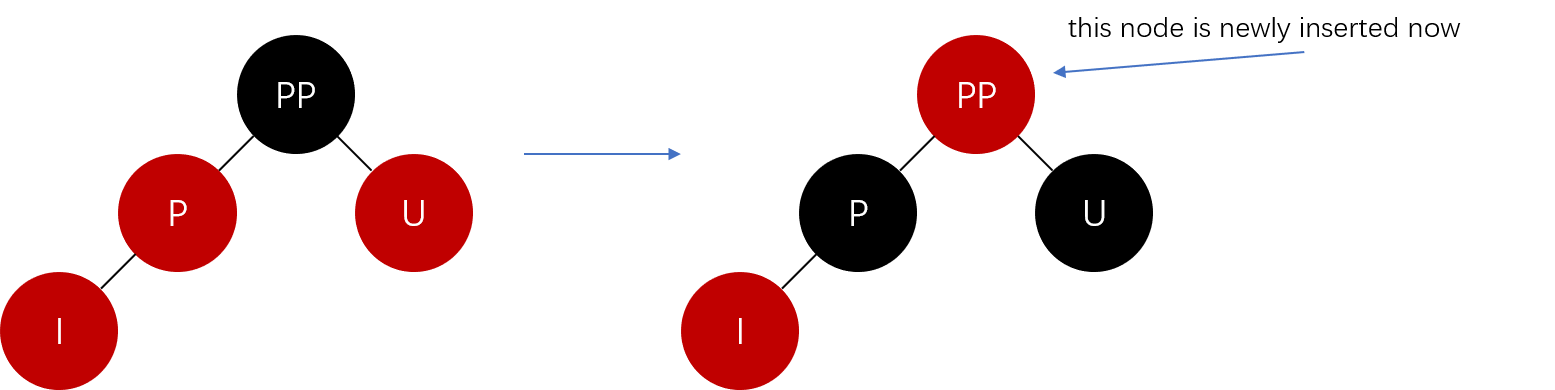 红黑树插入情况4.1

注：情况4.1是唯一一种会导致黑色高度增加的插入情况，因为最终会递归到双亲的双亲为根，这时不能将根改为红色，根保持黑色，因此黑色高度加1

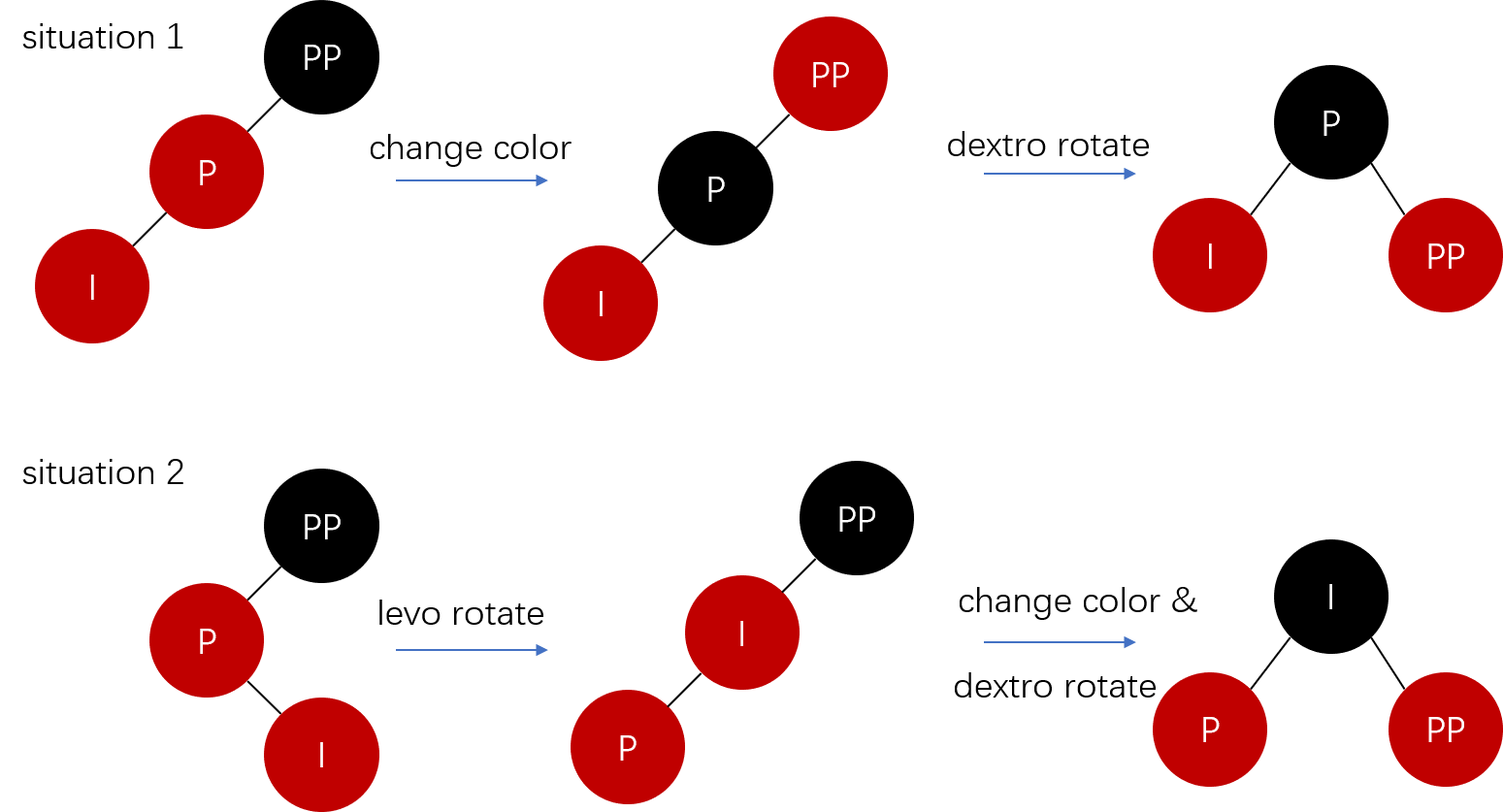
情况4.2：双亲节点没有兄弟节点

与4.1对比，这种情况按4.1处理会引起黑色平衡被破坏(插入节点一侧的黑色高度不变，但另一侧减少)，因此需要用左/右旋来重新达到黑色平衡。可能出现的情况如下图，其中和4.1一样，省略一些可以类推的情况 红黑树插入情况4.2

删除

删除可以大致分为两步

  1. 按照普通二叉排序树的删除进行，即将任意一个节点的删除转化成叶子节点(这里指的不是NIL节点)替换这个节点并删除叶子节点，这样有利于简化删除的情况讨论
  2. 将叶子节点删除后，需要进行相应的调整(左/右旋、变色)来让新的树符合红黑树定义

    普通二叉树删除

  3. 某节点无孩子(不包括叶子NIL)，那么直接删除
  4. 某节点只有一个孩子，删除该节点后，用孩子节点替代这个节点(指替代位置并修改成该节点颜色)
  5. 某节点有两个孩子，那么用直接后继替代该节点；如果直接后继节点有右孩子(不可能有左孩子)，那么再按2进行一次

注：上述删除过程中，不会引起红黑颜色节点不合法的父子关系，因为替代原节点位置的同时还要修改颜色为原节点颜色，必然符合定义

新树的调整

进行普通二叉排序树删除之后，下一步就是变色、旋转从而调整树使其满足

双重黑色

由于按照普通二叉树删除后，当删除节点(指x，即最终等效删除的节点)是黑色节点时，会引起x新所在位置(即y位置)所有祖先不符合黑色完美平衡要求，因此可以将x视作带有双重黑色，这样依然满足黑色完美平衡

2.1.x为红色

处理方法：删除红色节点不会影响树的黑色平衡，因此

应用

参考