Graph

1.图基本概念

图的基本概念包括：

• 有向图、无向图
• 边权、网
• 简单图、多重图
• 完全图(简单完全图)
  无向完全图有n(n-1)/2条边，有向完全图有n(n-1)条弧
• 子图
• 连通性、连通图、连通分量：
  极大连通子图称为连通分量，一般是唯一的(对于连通图来说就是本身)，但是也存在不唯一的情况，例如非连通图可以有两个完全相同的连通分量。
• 强连通性、强连通分量
• 生成树、生成森林：
  生成树其实是包含所有顶点的极小连通子图

极大连通子图和极小连通子图的意义为边极大、极小，连通图的极大连通子图是其本身，极小连通子图一般只对连通图而言

• 度、出/入度
• 稠密图、稀疏图：e < vlogv时
• 路径、路径长度、回路(环)
• 简单路径、简单回路：
  没有重复顶点的路径是简单路径，除了起点终点相同、其他顶点均不相同的回路是简单回路
• 距离
  最短路径长度
• 有向树
  只有一个顶点入度为0，其余顶点入度均为1的有向图，并且其对应无向图是连通的

2.图的存储结构

图的常用存储结构包括：邻接矩阵、邻接链表、十字链表、邻接多重表、边表

2.1.邻接矩阵

邻接矩阵即二维数组，如果顶点为结构体，还需要设置顶点数组存储顶点信息

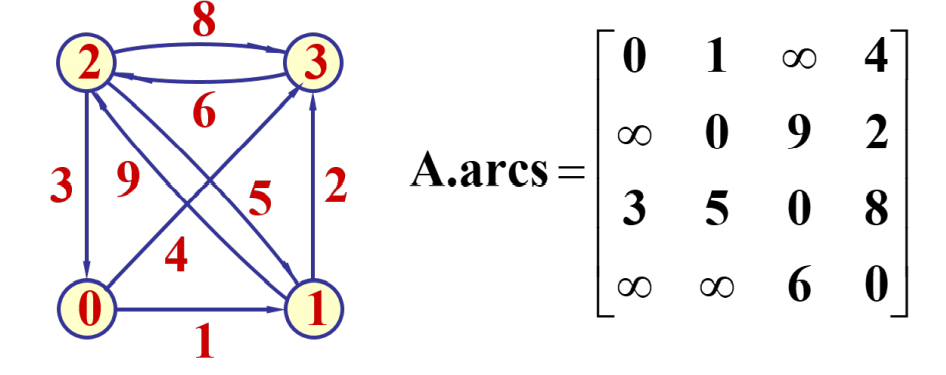
注意：对于有向图，上图中邻接表行为起点，列为终点，但也可以根据需要设置。对于带权图，不相关联的点边权置为INF或者0，根据具体需要，例如最短路径算法置为INF更方便；对于不带权图，同理。

#define MAXSIZE 100
#define INF 999
#typedef enum {DG,UDG,DN,UDN}GraphType;
typedef struct _arccell{
  ArcType w;//边权值
  InfoType * info;//边信息 
}ArcCell, AdjMatrix[MAXSIZE][MAXSIZE];

typedef struct _adjgraph{
  AdjMatrix arc;
  VexType vex[MAXSIZE];
  GraphType kind;
  int vexnum,arcnum;
}AdjGraph;

2.2.图的邻接表

图的邻接表即顶点数组加边链表

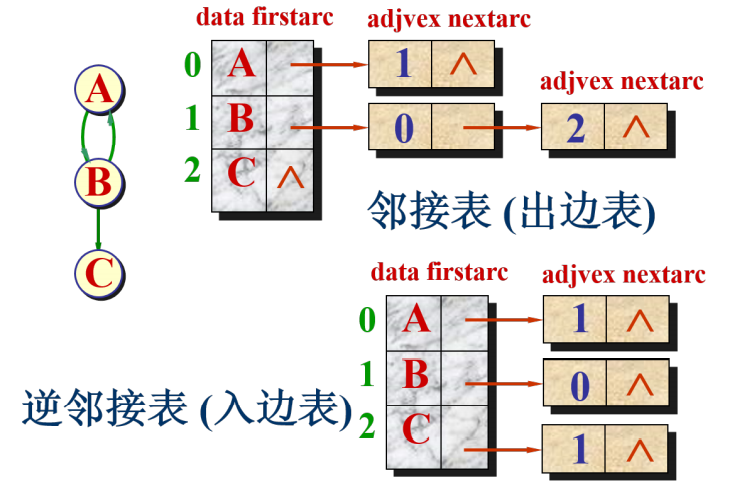
代码实现：适合稀疏图

#define MAXSIZE 100
typedef struct _arcnode{
  ArcElemtype w;
  InfoElemtype * info;
  int adjvex;//相关联的另一个节点，注意这里用顶点数组下标表示这个点
  struct _arcnode * nextarc;
}Arcnode;

typedef struct _vexnode{
  VexElemtype data;
  Arcnode * firstarc;
}Vexnode;

typedef struct _algraph{
  GraphType kind;
  int vexnum, arcnum;
  Vexnode vex[MAXSIZE];
}ALGraph;

有向图的十字链表

出边表+入边表，边节点合并，增加节点内容即可实现；绘制时先绘制出边表（邻接表），再补充入边表。

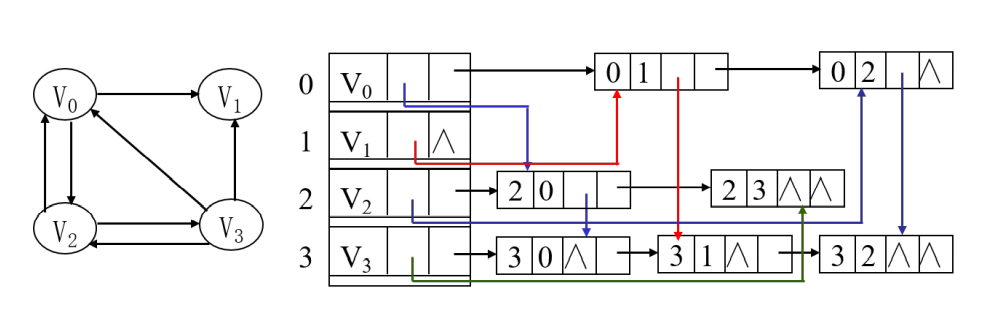
有向图的十字链表和稀疏矩阵的十字链表本质上是一样的，前者节点的出边域和入边域分别构成了后者的行、列数组，前者的边节点对应后者的矩阵元素

代码实现：与邻接表相似

#define MAXSIZE 100
typedef struct _arcnode{
  ArcElemtype w;
  InfoElemtype * info;
  int headvex, tailvex;//该边的头和尾（头指的是箭头终点），注意和邻接表一样，用节点数组的下标来表示
  struct _arcnode * hlink,* tlink;//指向下一个入边/出边结构体的指针
}ArcNode;

typedef struct _vexnode{
  VexElemtype data;
  ArcNode * firstin, *firstout;//指向第一个入边/出边的指针
}VexNode;

typedef struct _olgraph{
  GraphType kind;
  VexNode vex[MAXSIZE];
  int vexnum,arcnum;
}OLGraph;

无向图的邻接多重表

边节点合并的邻接表，增加边节点的内容即可

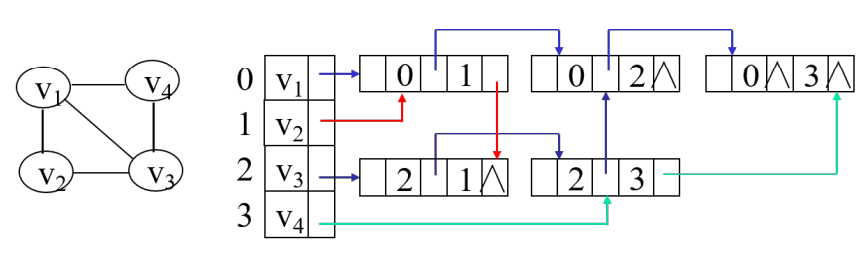
代码实现：与邻接表相似，适合于注重边的遍历、访问、搜索的算法，原因是邻接表访问过需要在两个边节点上做标记，非常麻烦，而邻接多重表只需要在一处标记。

#define MAXSIZE 100
typedef struct _arcnode{
  int mark;//访问标记，标记是否被访问
  int iadjvex;//一个端点 
  struct _arcnode * ilink;//下一个与i端点相连的边节点的指针 
  int jadjvex; 
  struct _arcnode * jlink; 
  ArcElemtype w;
  InfoElemtype * info;
}ArcNode;

typedef struct _vexnode{
  VexElemtype data;
  ArcNode * firstarc;
}VexNode;

typedef struct _amlgraph{
  GraphType kind;
  VexNode vex[MAXSIZE];
  int arcnum, vexnum;
}AMLGraph;

3.图的搜索和遍历

4.图的应用

4.1.最小生成树算法

Prim算法

• 算法思想：一端在U，另一端在V-U的边中，最小边加入生成树内
• 算法图解：
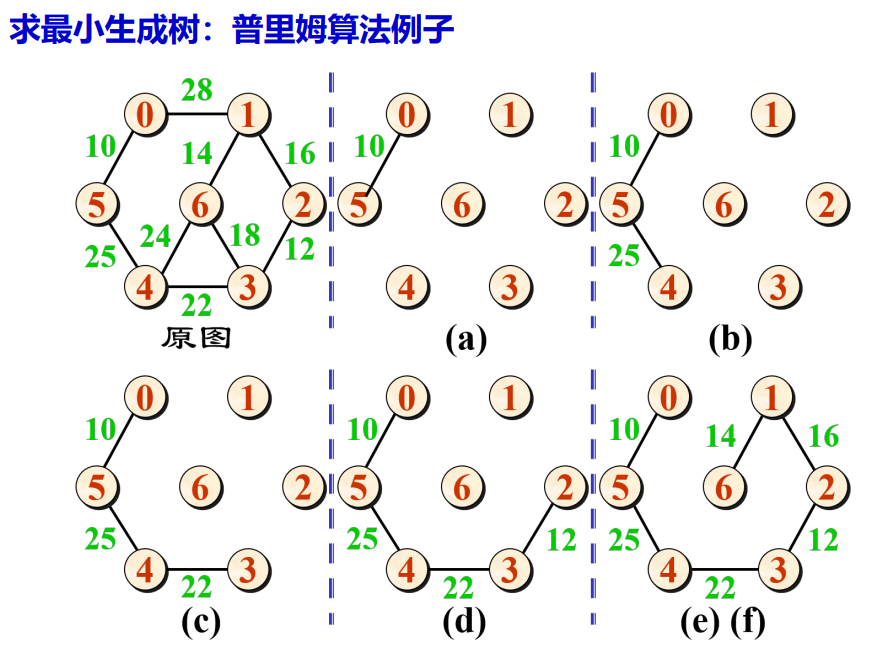
• 算法时间复杂度：O(n^2)，原因：，采用邻接矩阵实现，n次循环，每次循环需要检查新加入顶点的所有边从而更新存储各点对应最小边的辅助数组
• 算法输出结果：边权均不同，输出唯一的最小生成树。有相同边权，可能不唯一。

Kruscal算法

• 算法思想：对所有边进行排序，依次选择最短的边且不产生环，直到所有点处于同一连通片（有相同的连通片编号）。
• 算法图解
  
• 算法时间复杂度：O(eloge)，原因：对边排序，然后对边依次处理

4.2.AOV网络（有向无环图）与拓扑排序

• 定义：AOV网络是无环的有向图，其顶点表示活动，弧表示活动的先后顺序
• 拓扑排序：
  • 定义：将各顶点排列成线性有序的序列，检测AOV网络是否有环（有向环不允许出现在AOV网络里，即AOV网络没有强连通分量）;不能给出拓扑全序的AOV网络表示一项不可行的工程。
  • 算法思想：删除并输出入度为0的点，同时删除其出边，重复算法直到所有点都被输出。
  • 算法实现：用邻接矩阵或者邻接表表示有向图，栈存放入度为0的点，出栈执行删除出边和入栈操作；最终输出点个数少于AOV网络顶点个数，存在环。此算法可以用来检测网络是否存在环。
  • 算法时间复杂度：O(n+e)，原因：统计各顶点的入度，顶点指针移动n次，而边指针总共移动e次，复杂度为O(n+e)；排序过程顶点入栈出栈均为n次，删除边e次，故最终时间复杂度为O(n+e)。

思考：
1.如果拓扑序列是有序的(指节点编号有序)，那么图的邻接矩阵是什么样的？
答：是上/下三角的
2.什么样的点不能出现在拓扑序列中？
答：既是起点又是终点的节点

4.3.AOE网络

• 定义：AOE网络是无环的有向图，弧表示的是活动，顶点表示事件，每个事件表示其前的所有活动已经完成，其后活动可以开始。
• 关键路径与关键活动
• 定义：关键路径指从开始点到终点最长的路径，其实际上是整个工程完成的最短时间（因为某些活动可以并行）。在关键路径上的活动是关键活动，其最早开始时间和最晚开始时间相等，提前完成非关键活动并不能加快工程的进度。
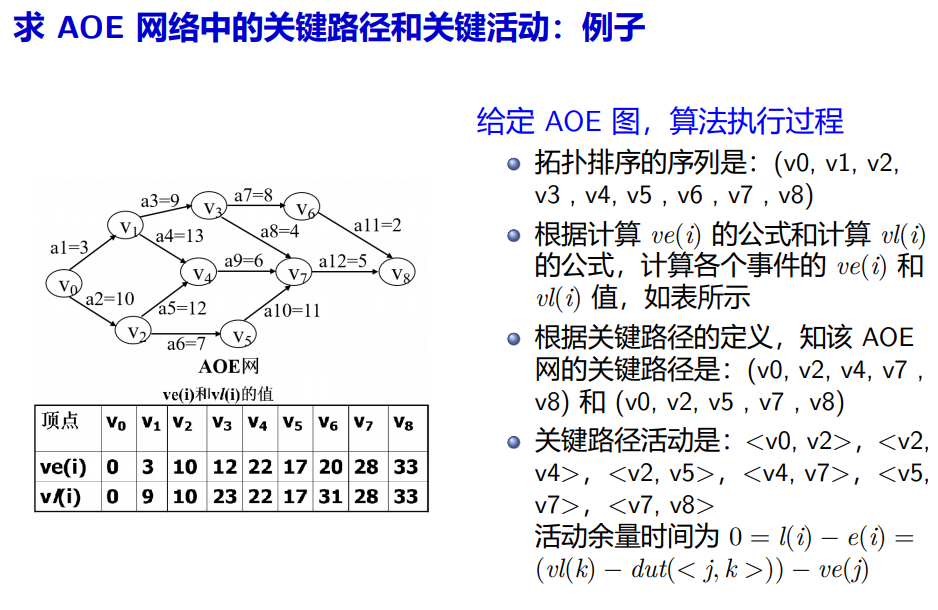
• 求解算法：求出拓扑序列
  求各事件最早发生时间ve(i) = max{ve(j) + dut(i,j)}，j处于拓扑序列中i之前，即从起点到i的最长路径，因为如果不是最长的路径，无法保证i的前置活动全部做完。
  求各事件最晚发生时间vl(i) = min{vl(j) - dut(i,j)}，j处于拓扑序列i之后，即从终点到i的逆向最长路径，因为如果不是最长的路径，无法保证i后续事件时间是充足的。根据ve和vl求出关键路径。

• 算法时间复杂度：O(n+e)，原因：拓扑排序O(n+e)，求ve总共要遍历整个邻接表一次来不断更新ve，求vl同理，时间复杂度O(n+e)。

4.4.最短路径算法

Dijkstra算法

• 算法思想：使用最新确定最短路径的点i去更新起点到未确定点最短路径列表，更新后列表最小点被加入已确定点列表。
• 算法时间复杂度：O(n^2)，原因：n次循环，每次都要在当前未确定距离中找到最小的

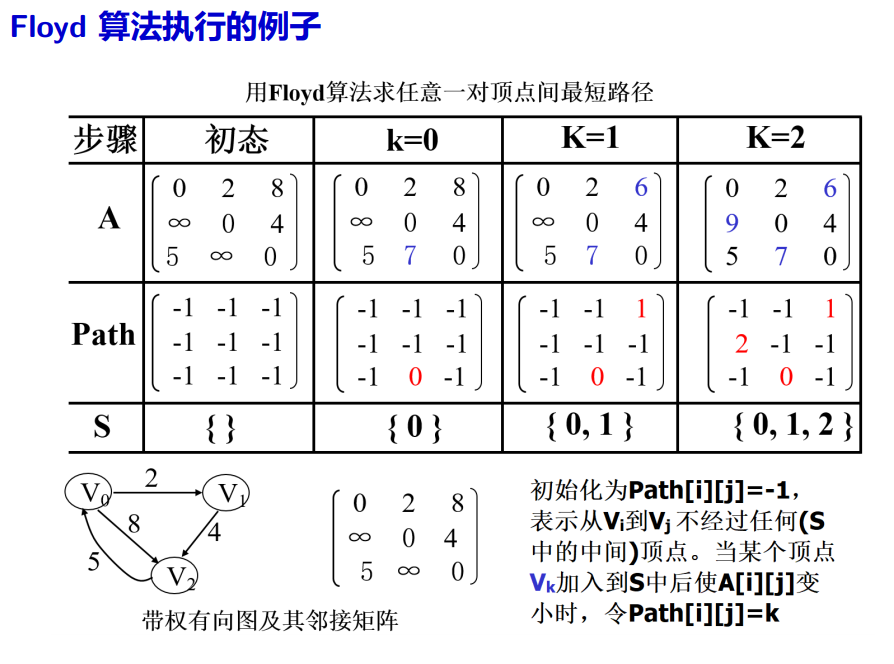
Floyd算法

• 算法思想：初始化数组A等于邻接矩阵，P为全-1。将v0作为中间节点，更新数组A最短路径，并在P[i][j]内记录v0（即i通过v0到j最短，路径为iv0j）。再将v1作为中间节点，重复上述步骤，直到重复n次。
• 算法时间复杂度：O(n^3)，原因：三重循环，最外层循环负责每次将一个点作为中间节点，内部双重循环用于计算ivj并更新。