特殊矩阵/Special Matrix
基本定义
特殊矩阵指的是0和非零元素分布有一定规律的矩阵
对称、对角矩阵
对于对称矩阵、二对角矩阵、三对角矩阵:顺序压缩存储映象函数的求解?
解法:一般为线性关系,通过 k = ai + bj + c 解方程来求解
稀疏矩阵
非零元素远少于0元素的矩阵
数据结构实现
顺序存储实现:三元组表(Triple)
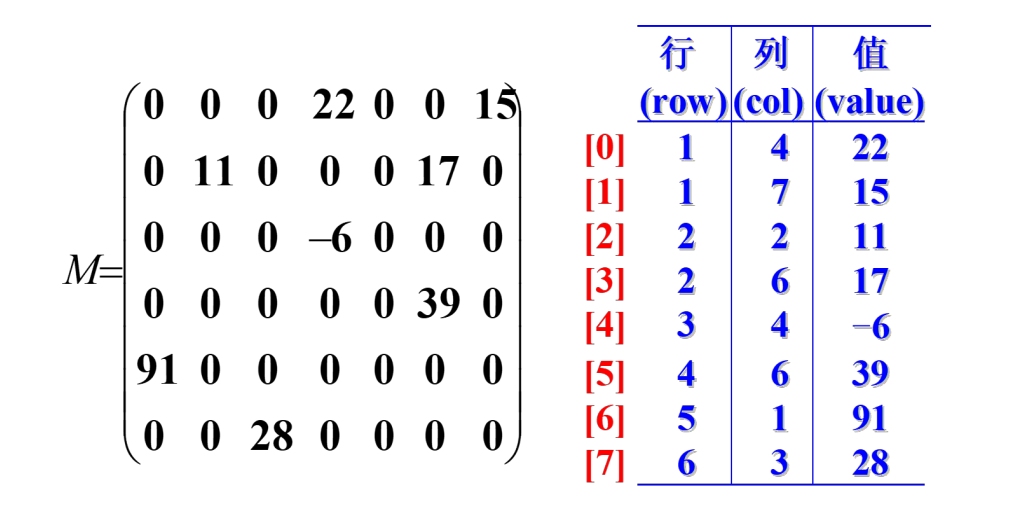
代码实现:带先后顺序结构体数组
#define MAXSIZE 12500
typedef struct _triple{
Elemtype e;
int i,j;
}Triple;
typedef struct _tsmatrix{
Triple data[MAXSIZE+1];//索引0处未用,行为主序(行数小的在前面)
int mu, nu, tu;//行数、列数、非零元素数
}TSMatrix;
三元组表实现矩阵转置操作
- 方法1:先交换行号和列号,再按照行先序、列次序的顺序进行排序
- 方法2:从列号j=1开始,重复从前往后搜索列号等于j的元素(先搜索到的元素行号更小),然后放入新的三元组表内,对j=1到j=n循环。时间复杂度O(tu*nu),即每次都要搜索表,要搜索nu次
### 链式存储实现:十字链表

代码实现:两个指针数组+一堆链表节点相连
typedef struct _olnode{
Elemtype e;
struct _olnode * down, *right;
int i,j;//该节点的行、列数,设置此域是为了方便建立十字链表的时候找到插入节点的位置
}OLnode;
typdef struct _crosslist{
int mu,nu,tu;//行数、列数、非零元素数
OLnode ** chead, rhead;//列指针、行指针数组
}CrossList;
十字链表的优点
对于需要大量移动非零元素位置的操作,十字链表比三元组表更加容易。例如转置(十字链表每一行递归交换down和right指针以及行、列域值即可,三元组表交换节点的i、j后,还需要重新排序)、等于x的元素置零(每一行递归实现,递归过程中记录递归来源节点的指针从而修改链表连接关系,例如将上一个节点的right指针指向被置零节点的right;完成后再每一列递归实现,这一次只需修改指针关系而不需要赋值)等操作
注意事项
- 绘制三元组表要注意如果行/列为主序,那么列/行为次序,而不是随意排序
- 绘制十字链表注意节点包括行、列、节点value和down、right五个域