Sort

内部排序

概念：待排序记录存放在随机存储器内的，在随机存储器内进行排序的过程

插入排序

基本实现：0处设置监视哨，将第i个元素插入前i-1个元素的有序序列内，同时从后向前移动元素，完成后i++

折半插入排序

基本实现：查找位置不再从后向前查找，而是折半查找

希尔排序

基本实现：构造”基本有序”序列，插入时增量移动而不是一个一个位置移动

注意：希尔排序涉及到增量序列的选择，其性能与增量序列有关

冒泡排序

基本实现：相邻元素比较，不断交换元素至最后一位，若无元素发生交换则停止

快速排序

基本实现：将第一个元素起泡至当前序列某位置(过程中将低位大元素移到高位，高位小元素移到低位)，然后分别对两个子序列重复

栈空间的改进

利用循环(只进行两次的循环)，先执行较短子序列的调用，从而进行尾递归

选择排序

基本实现：前i-1个最小元素已排列好，从后h-i+1个元素中选出最小的，与第i个元素交换，然后i++，即不断选出第一小、第二小…的过程

树型选择排序

基本实现：元素两两比较构造一棵胜者树(锦标赛)，根为冠军，输出根后将根对应的叶子改为INF，再进行树的构造，注意：未修改的另外一个子树不需要做任何操作，比较结果直接复用

堆排序

基本实现：与树型选择排序类似，但构造堆直接从数组下标关系得到完全二叉树，然后从最后一个非终端节点调整；输出根之后，用树的最后一个元素(数组存储的树中最后一个元素)替换根，然后调整树得到新堆（重复筛选）

建堆和筛选的方法/示意图

归并排序

基本实现：将元素两两归并，然后将有序段两两归并，重复直到整个数组有序

基数排序

多关键字排序

实现方法

MSD/最高位优先：先按最主位关键字分堆并排序，然后堆内按次关键字分堆并排序，重复直到对最次关键字分堆并排序，注意：除了第一次，每次都是在对某个子序列排序
LSD/最低位优先：先对最次关键字排序，然后对高一位关键字排序，直到对最高位关键字排序，注意：每次都是整个序列在参与排序，但是在逐渐变得部分有序

链式基数排序

基本实现：把单逻辑关键字视为多关键字的复合，然后从最次关键字开始，按照队列顺序，分配并收集，再按照新队列顺序，分配并收集，直到对主关键字分配收集，得到有序序列

基于比较的内部排序算法最坏时间复杂度证明

证明方法：判定树，其叶子为n!种可能的初始状态，那么树高为log(n!)，即O(nlogn)

各种内部排序算法的比较

排序算法	插入排序	折半插入排序	希尔排序	冒泡排序	快速排序	选择排序	树型选择排序	堆排序	归并排序	基数排序
分类	插入排序	插入排序	插入排序	冒泡排序	冒泡排序	选择排序	选择排序	选择排序	归并排序	基数排序
平均时间复杂度	O(n²)比较和移动	O(n²)移动(不变，该移动多少移动多少)，O(logn)比较	O(n^k)，1&ltk&lt2，取决于增量序列选取	O(n²)比较和交换	O(nlogn)，并且是同数量级排序算法中最快的	O(n²)	O(nlogn)	O(nlogn)	O(nlogn)	O(d(n+rd))
最好时间复杂度	正序序列：O(n)比较，无数据移动	正序序列：O(logn)比较，无数据移动	N/A	正序序列：O(n)比较，无数据交换	O(nlogn)	O(n²)，正序序列数据交换变少，但是比较次数不变	O(nlogn)，和平均相同，永远是一棵均衡的二叉树	O(nlogn)	O(nlogn)	O(d(n+rd))
最坏时间复杂度	逆序序列：O(n²)比较和移动	逆序序列：O(n²)移动，O(logn)比较	N/A	逆序序列：O(n²)比较和交换	正序序列/基本有序：O(n²)，退化成冒泡排序	O(n²)，比较次数和初始状态无关	O(nlogn)，和平均相同，永远是一棵均衡的二叉树	O(nlogn)	O(nlogn)	O(d(n+rd))
稳定性	稳定	稳定	不稳定，例如两相同元素在某增量对应不同序列里	稳定	不稳定，例如高位某小元素和支点交换，和支点相等元素没动	稳定	稳定	不稳定	稳定	稳定
辅助空间	O(1)	O(1)	O(1)	O(1)	O(logn)	O(1)	O(n)，即一棵二叉树	O(1)	O(n)，存储归并结果	O(rd+n)，队列指针和各元素的指针
适合场景/优点	n很小时、基本有序时的简便排序方法	相比简单插入减少了一些比较次数	增量移动从而构造基本有序序列，最后一步插入排序更快	简单	平均最快	简单	相比选择排序利用了前一轮的比较结果	相比选择排序利用了前一轮的比较结果，并且最差时间复杂度优于快速排序	与堆排序和快排相比是稳定的，并且n较大时比堆排序快一些	适合n较大且关键字较小的场景，并且基于分配收集而不是比较移动
备注/缺点	N/A	N/A	N/A	N/A	尾递归改进栈深度从最差O(n)为O(logn)	无论如何比较次数都是O(n²)	辅助存储空间需求大、INF重复比较	N/A	辅助空间要求大，并且递归形式需要栈空间	N/A

外部排序

一般方法

分成m个初始段并每一段内部排序，然后k路归并。每次从外存中读取k个block的数据放入k个内存缓冲区，归并结果写入一个内存缓冲区内，写满则进行I/O从而落盘

总时间计算

初始段内部排序：m*t₁，m为段数
总读写时间：t₂*(2*(归并趟数+1)*记录数/块大小)，加一是因为初始段内部排序还需要对所有记录进行“一趟”读写
每一趟归并的时间与趟数乘积：趟数*记录数*t₃，t₃为平均对每个记录归并消耗的时间，它和路数有关
- 注意：对长m和长n的段进行2路-归并的时间为O(m+n)，所以归并时间只和总记录数和路数有关
总时间主要和读写时间有关
- 读写时间计算：每一趟归并读写次数是固定的，因为总记录数量确定。对于k叉树，叶子m个，树高为min(log_km)+1，归并趟数为min(log_km)
  - 总读写时间：O(log_km)，其中k为归并路数，m为初始段数量

多路平衡归并

基本思想：增加路数k以减小读写时间

基础实现

增大k，但是这样会导致每一趟内部归并时间变长

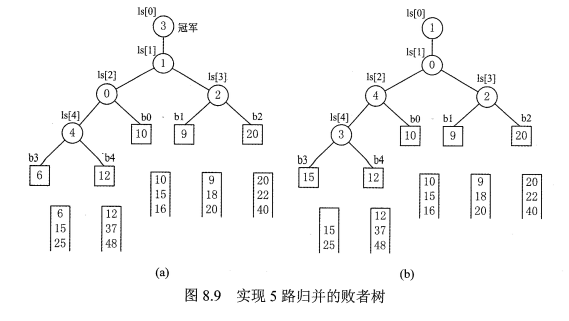
进阶实现：败者树

败者树，即利用上一次归并已比较的元素的结果

败者树：内部节点记录败者信息，与树型选择排序胜者树相反，好处在于当叶子发生变化时，只需要与父亲比较而不需要先找到父亲再找到兄弟比较，减少读写次数(对于外存来说收益大，若都在内存减少的收益有但不大)
时间复杂度：
- 单次归并/平均每个元素归并时间：
  - 除了建树，每次归并比较次数为log₂k，因为只需要在上次结果所处的半边子树进行调整，最后在根处和另一个子树的结果(败者)比较即可
- 总内部归并时间：s*(n-1)*log₂k = (n-1)*log₂m，与路数无关，所以增加k不会引起内部归并时间上升(m不变)
实现细节：归并段若变空，那么可以在归并段最后添加MAX/MIN

优缺点

优点：
- 增加了路数并使用败者树，在减少读写次数(其实是减少归并趟数)的同时保证总的内部归并时间不会因为路数上升而上升
- 注意：单趟读写次数不变，并且单趟、单次归并比较次数还是会上升的
缺点：需要增加内存缓冲区的大小，如果k过大，单个内存缓冲区变小，读写次数反而上升

置换-选择排序

基本思想：减少归并段数量/增加归并段长度

原本的实现

归并段长度等于内存工作区长度w，故有n/w个初始段

置换-选择排序

原理：归并段不等长，且平均长度大于w，因此趟数减少(假设路数k不变)
实现
- 向工作区读入w个记录，然后构造败者树，并且将冠军写入输出文件
- 顺序读取下一个记录，如果其大于上一个冠军，段号不变；如果其小于上一个冠军，其段号是下一段；调整败者树，将冠军写入输出文件，此时如果段号发生变化，证明前一段已经排序好。这一步实际上在选择不上一个冠军大的工作区内最小记录，如果没有那么这一次的冠军是下一段的开头。
- 重复上一步直到输入文件空
归并段平均长度：2w，对于随机数序列来说
- 证明：“扫雪车“证明
  工作区记录是积雪，输出的记录是扫走的雪，新进入的记录是新下的雪，其分布概率大于/小于输出记录各一半，即积雪落在扫雪车前和后概率相等。那么一圈得到一段，扫走的雪是当前积雪量(一个斜面)的两倍
时间复杂度：O(nlogw)，这和普通的分段方法相同，即n/w *wlogw=nlogw

最佳归并树：利用置换-选择排序的结果

一般实现：平衡归并树，其趟数已经比普通的分段方法少
进阶实现：最佳归并树
- 理解：霍夫曼树，带权路径是读写次数，比平衡树读写次数少
- 非完美k叉树
  - 虚段：即长度为0的段，对于霍夫曼树必然是第一次归并
  - 虚段判定：
    - 无需虚段：完美k叉树满足(k-1)n_k+1=n₀，故n₀-1MOD(k-1)=0
    - 需要虚段：k-1-(n₀-1)MOD(k-1)个，即第一次归并是1+(n₀-1)MOD(k-1)路归并(虚段无需参与归并)
      - 原因：余数为t，那么即(k-1)(n_k-1)+t=n₀-1，因此(k-1)n_k = n₀-1+(k-1-t)